Some situations call for prioritizing memory usage over performance. We may be willing to sacrifice some performance if it helps us save space. Either we have limited space to store data. Or we have limited bandwidth to transfer it.

Let us look at a simple example: DNA sequences. Suppose we have an enormous dataset of DNA sequences. And we want to serve them over HTTP with a web API.

How data is kept in memory

Using Python, given an object, we can find out how much space (in bytes) it uses.

print(sys.getsizeof(1)) # 24

That means that we are using 24 bytes for a single number. We may want to use an array of numbers:

print(sys.getsizeof([])) # 72
print(sys.getsizeof([1])) # 80

What? An empty array by itself takes 72 bytes.

In Python, every type is an instance of an object. Which has extra properties and methods. For example, we can call the .toString() method on many of these objects.

A naive approach to modeling a DNA sequence

We can represent our DNA sequence as a string made up of four letters "A", "T", "G", "C". Each represents a DNA nucleotide, the distinct molecules that make up DNA.

print(sys.getsizeof("A")) # 50 
print(sys.getsizeof("AA")) # 51

Python uses 50 bytes for a one-character string, and one extra byte per character. For a JSON response, a single unicode character may take from 1 byte (8 bits) up to 4 bytes.

The most space-efficient approach

Turns out we only need to store a sequence of four distinct symbols. This is because there is a one-to-one map between the set of nucleotides and a set of four symbols.

\[ \{ A, C, G, T \} \rightarrow \{ 00,01,10,11 \} \]

Therefore, we need two bits to store a single nucleotide. As well as the mapping rule. This mapping rule defines a compression algorithm, from strings to bit-strings. And a decompression algorithm, from bit-strings to strings.

Using this approach we will end up sending 2 bits instead of 8 over the wire. That is a 75% decrease in space!

Implementing the compression algorithm

We can store the DNA sequence as a bit string. An arbitrary-length sequence of 1s and 0s.

def compress_gene(gene:str) -> int:
    bit_string: int = 1
    for nucleotide in gene.upper():
        bit_string <<= 2 # shift two bits left
        if nucleotide == "A":
            bit_string |= 0b00
        elif nucleotide == "C":
            bit_string |= 0b01
        elif nucleotide == "G" :
            bit_string |= 0b10
        elif nucleotide == "T" :
            bit_string |= 0b11
        else :
            raise ValueError(f"Nucleotide {nucleotide} is invalid!")
    return bit_string

Using Python, we can use a regular int as a bit string. Note that we are using bitwise operators. We want the bits used to store the int. Not so much the number itself.

Let's also look at the decompression function:

def decompress_gene(bit_string: int) -> str:
    gene: str = ""
    for i in range(0, bit_string.bit_length() -1 , 2) :
        bits: int = bit_string >> i & 0b11 # read the next two bits
        if bits == 0b00:
            gene += "A"
        elif bits == 0b01:
            gene += "C"
        elif bits == 0b10:
            gene += "G"
        elif bits == 0b11:
            gene += "T"
        else:
            raise ValueError(f"Invalid bits: {bits}")
    return gene[::-1] ## Reverse the decompressed string

The one-to-one mapping we identified above guarantees that a decompression algorithm exists. Let's see why.

Interlude: Mathematical gibberish

The one-to-one mapping is also known as a bijection. Consider a function \(f(x)\) between sets. It is injective if every element of its domain maps into a unique element of the codomain. If the same function also has every element of its codomain mapped to, we say it is surjective. If a function is both injective and surjective, we say it is a bijection.

Our nucleotides-to-2-bit-binary function is plain-as-day bijective.

Here's a corollary of a function \(f\) being bijective. We can guarantee the existence of a function \(f^{-1}\), that "undoes" whatever \(f\) does.

The important bit for programming is this. Many algorithms involve some kind of mapping between sets. If you can prove that mapping is a bijection you get the reverse algorithm for free.

If we understand these kinds of properties we can reason about, and prove (up to a certain extent) the behavior of programs. A less trivial example would be encryption. Prove that a hashing function is injective and you prove that it has no collisions. Alas, for many hashing functions, we can prove that they are not injective. We may then assess the probability of collisions as a way of measuring how strong they are. More about this in future posts :)

Assessing our program

Let's go back to our DNA example. We can write a simple test to see our algorithms in action:

def test_compress():

    original: str = "AATCGTAGCCA" * 10
    compressed: int = compress_gene(original)
    decompressed: str = decompress_gene(compressed)

    print (f"size of original: {sys.getsizeof(original)}")
    print (f"size of compressed: {sys.getsizeof(compressed)}")
    print (f"size of decompressed: {sys.getsizeof(decompressed)}")

    print (f"original: \n {original}")
    print (f"decompressed: \n {decompressed}")

    print (f"original and decompressed are the same: {original == decompressed}")

And the results:

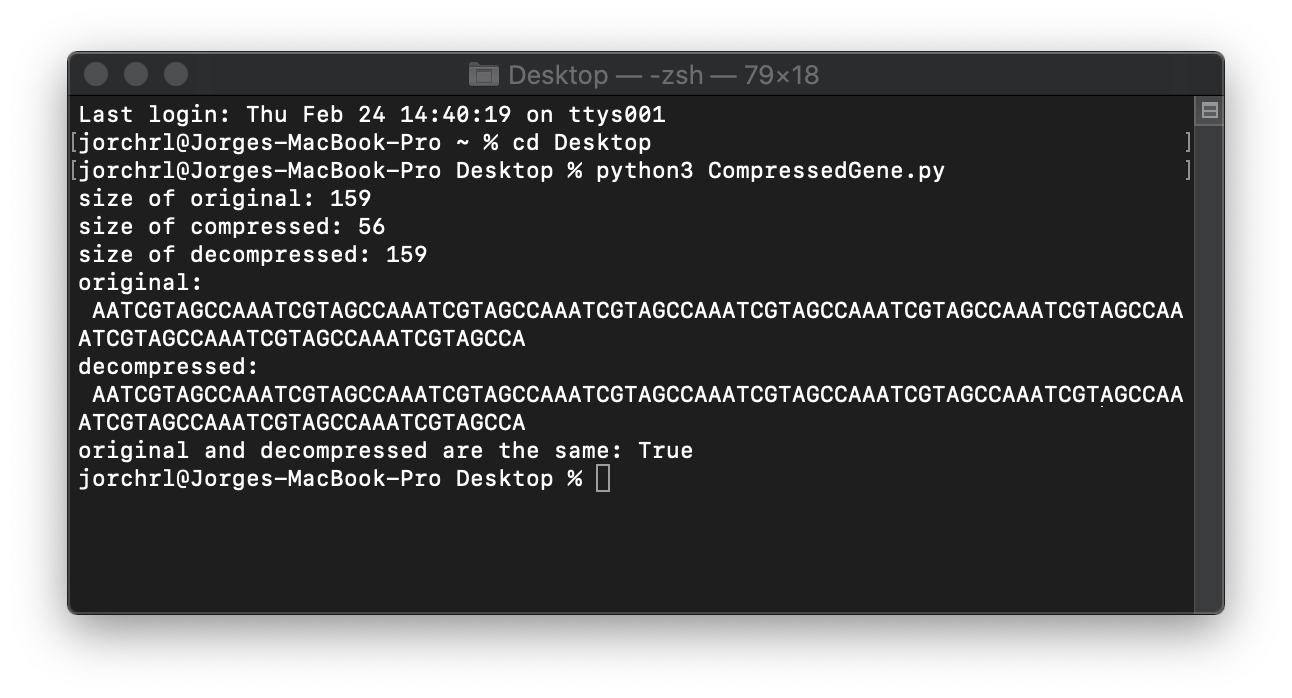
Recap

We saw a general programming tool, compression. And the kind of tradeoffs it entails: optimizing memory at the cost of processing power.

We also briefly discussed a mathematical tool: bijections. Which guarantees that an inverse of a function between sets exists. If we prove that an algorithm performs a mapping that is a bijection, we guarantee that an "undoing" algorithm exists.

As a little bit of computer science trivia, we used bitwise operations to use an int as if it were a plain bit string.

Hopefully, you found this post useful, interesting, or at the very least, pleasant to read. Any feedback is greatly appreciated!

See you in the next post! :)